Principe de fonctionnement d’une caméra Infrarouge (IR)
Le module FLIR Lepton 3.5 permet de récolter des données thermiques dans un environnement tri-dimensionnel. Il est important pour nous de comprendre comment fonctionne une caméra thermique ou infrarouge (IR) pour pouvoir exploiter au mieux notre module. Nous allons donc ici essayer de comprendre et d’apprendre les principes et fonctionnement d’une caméra infrarouge.
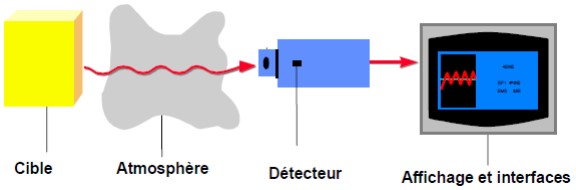
La caméra IR se compose, à la base, d’un radiomètre IR, d’un détecteur et d’un objectif thermique ou optique. La mesure par infrarouge consiste à ce que l’objectif focalise les radiations de l’objet que l’on souhaite mesurer vers le détecteur. De manière simple, ce fonctionnement peut se schématiser de cette manière :
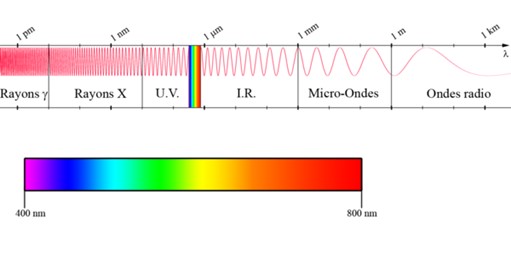
Le spectre électromagnétique
Tout corps ayant une température supérieure au zéro absolue (0 K ou -273,15 °C) émet une énergie infrarouge spécifique à sa température. Cette émission a lieu dans toutes les directions de son espace environnant. L’énergie est provoquée par le mouvement des atomes. Cette dernière exprimée en Joules et ramenée à une seconde constitue la puissance de rayonnement ou flux énergétique émis φ, ce flux s’exprime en Watt. L’intensité de ce mouvement dépend de la température du corps étudié. Ces mouvements s’associent à des mouvements de charge qui génèrent des radiations électromagnétiques.
Dans notre cas, le domaine spectral concernant la thermographie infrarouge s’étend de 2 à 18 µm. Cependant, la thermographie infrarouge se concentre principalement sur les ondes courtes de 2 à 5,5 µm et sur les ondes longues de 7 à 18 µm.
Avant de parler de comment sont perçus les infrarouges par la caméra IR, il est important d’évoquer comment la caméra IR interprète la cible dans son environnement tridimensionnel.
La notion d’angles solides
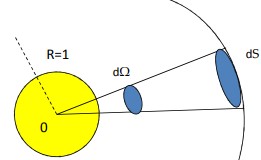
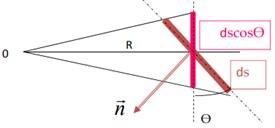
L’angle solide est l’analogue tridimensionnel de l’angle plan. Il correspond au rapport de la surface d’une partie d’une sphère sur le rayon au carré. Son unité est le stéradian noté « sr ». On peut le noter Ω. Il mesure la surface sur laquelle un objet se projette radialement sur une sphère de rayon unité.
\boxed{Ω=\frac{S}{R²}}
Avec Ω l’angle solide, S l’aire de la portion de sphère interceptée (m²) et R le rayon de la sphère (m).
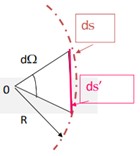
On peut aussi noter dS=dΩ.R^2 soit :
\boxed{dΩ=\frac{dS}{R²}}
Avec cette représentation, on a :
dS : surface vraie
dS’ : assimillée à une surface plane
Avec dS.cosθ la surface projetée.
\boxed{dΩ=\frac{dS.cosθ}{R²}}
Maintenant que nous avons défini l’angle solide, nous pouvons parler de l’intensité énergétique. Sa formule est :
\boxed{I=\frac{dϕ}{dΩ}} en W/sr
Cette intensité énergétique intervient dans la luminance énergétique L_λ.
Luminance énergétique L_λ
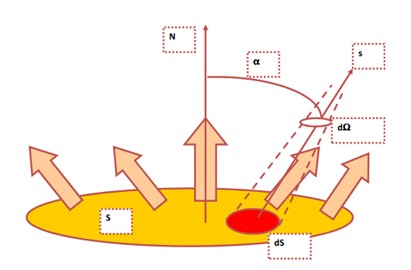
Pour comprendre son intérêt, considérons une surface S qui émet dans toutes les directions un flux énergétique φ. Une caméra IR est placée devant S afin de déterminer la température. Nous pouvons remarquer différents points quant au détecteur de la caméra :
- Il n’a en général en face de lui qu’un élément de la surface dS et non l’intégralité de S
- Il peut alors intercepter qu’une partie du flux énergétique φ, dans un angle solide Ω
- Il n’est pas nécessairement placé selon la normal N à la surface. On en conclut que la partie dS perçue est en fonction d’un angle α. Ce dernier correspond à l’inclinaison de l’axe de la caméra avec la normale N. On peut en déduire que l’élément réellement perçu a pour valeur dS.cos α.
- Il possède une certaine bande passante et donc ne réagit qu’à une certaine limite de longueur d’onde
La luminance énergétique se définit comme :
\boxed{L = \frac {dI} {dσ} =\frac {d²ϕ}{dΩ.dS.cosθ}} en W/(m².sr)
Elle représente le flux émis par une surface ramenée à 1m², dans un angle solide de 1 sr, lorsqu’elle est portée à une température T.
Elle permet de comparer la puissance rayonnée dans une direction donnée par des sources d’étendues différentes ou d’orientation différentes par rapport à cette direction ainsi que les puissances rayonnées par une même source dans différentes directions.
Emission du rayonnement
Nous venons de définir la luminance énergétique. Nous pouvons maintenant nous pencher sur l’émission.
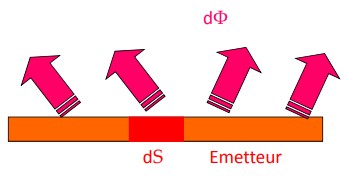
D’abord, nous devons aborder la notion d’émittance.
Elle se note de manière simplifiée M et peut se définir de la manière suivante :
\boxed{M_E = \frac{dϕ}{dS_E}}
Avec dS_E la surface de l’émetteur.
L’émittance énergétique totale est une notion importante pour comparer les densités de puissance réalisable avec différentes sources de rayonnement IR.
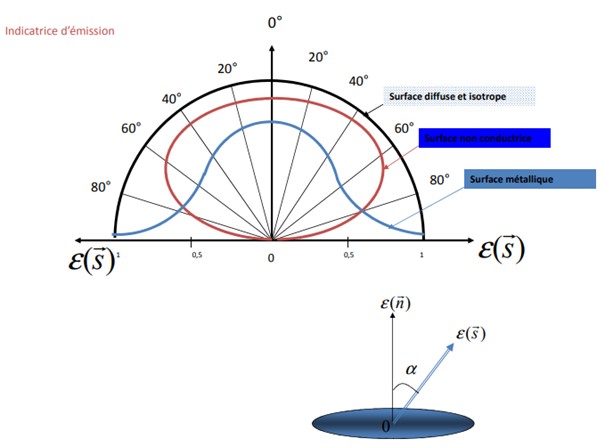
On dit que l’émission est diffuse (ou isotrope) si la luminance est indépendante de la direction entre le détecteur et la surface. On dit que la surface émettrice obéit à la loi de Lambert.
\boxed{M_E = π.L_E}
Cette relation montre l’importance de la position du produit par rapport aux émetteurs dans le cadre du rayonnement IR.
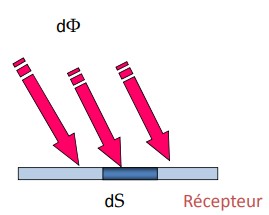
Absorption du rayonnement
On retrouve pour l’absorption une relation sensiblement identique à l’émission.
\boxed{E=\frac{dϕ}{dS_R}} en W/m²
Cette relation montre l’importance de la position du récepteur par rapport à l’émetteur dans le cadre du rayonnement IR.
Aussi, il est primordial de ne pas l’oublier l’importance de la distance entre l’émetteur et le récepteur. Il faut donc être attentif à la position de l’émetteur et du récepteur mais aussi à la distance qui les sépare.
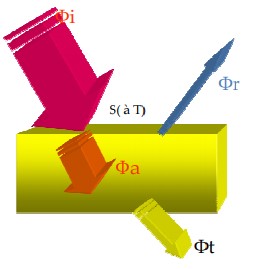
Nous comprenons alors qu’il existe un lien entre émission et absorption. La loi de Kirchhoff, nous dit que l’émissivité ε et l’absorptivité α d’une surface à une température et une longueur d’onde données sont égales. Il est possible de visualiser ce principe de la manière suivante :
Avec cette représentation, nous avons :
\boxed{α = \frac{ϕ_a}{ϕ_i}} Coefficient d’absorption
\boxed{ρ = \frac{ϕ_r}{ϕ_i}} Coefficient de réflexion
\boxed{τ = \frac{ϕ_t}{ϕ_i}} Coefficient de transmission
Et donc \boxed{α+ρ+τ=1}
Emissivité
Le terme ε(λ) caractérise le pouvoir émissif d’un corps. C’est-à-dire la partie restituée de l’énergie qui ne correspond ni à la réflexion ni à la transmission. Cela s’appelle l’émissivité spectrale du corps pour la longueur d’onde λ.
Pour un corps quelconque, elle est donnée par :
\boxed{ε_λ = \frac{L_λ}{L_λ^0}}
Avec L_λ : luminance énergétique du corps étudié
L_λ^0 : luminance énergétique du corps noir associé à la longueur d’onde et possédant la même température que le corps étudié.
Corps noir
Un corps noir se définit par un corps qui absorbe la totalité de l’énergie qu’il reçoit. On peut considérer cela comme une enceinte creuse et opaque (α = 1). Pour respecter l’équilibre thermique, il convient qu’elle émette autant qu’elle reçoit soit ε= α=1. Dans la pratique, on creuse un petit orifice dans l’enceinte et on analyse le rayonnement sortant. Ces corps noirs ne sont utilisés principalement qu’en laboratoire et servent à l’étalonnage ou le contrôle de fonctionnement des caméras IR.
Le flux de puissance total émis par un corps noir peut se déterminer avec la loi de Stefan-Boltzmann.
\boxed{M_0= σ.T^4} en W/cm²
Avec σ la constante de Stefan-Boltzmann et T la température en Kelvin.
Cependant la puissance définit par cette loi correspond à la puissance globale émise. En réalité, le corps n’émet pas également pour toutes les longueurs d’onde, la loi de Planck nous donne cette répartition :
\boxed{M_((λT) )= C_1*λ^{-5}*\frac{1}{e^{\frac{C_2}{λT}}-1}}
Avec C_1=3,74*10^{-16} W.m² et C_2=1,438*10^{-2} m.K
Corps gris
Un corps gris peut se définir en disant que c’est un corps où l’émissivité ne varie pas en fonction de la longueur d’onde. Dans la pratique, la grande majorité des corps sont « gris ». On peut alors écrire que l’énergie monochromatique devient :
\boxed{M_{λT}=ε_{λT}*M_{λT}^0}
Donc, pour un corps gris, la puissance Φ émise sous forme de rayonnement peut s’écrire :
\boxed{Φ=ε*S*σ*T^4}
ε : émissivité comprise entre 0 et 1
S : surface du corps
T : température en Kelvin
La loi de Wien permet de faire une approximation de la loi de Planck.
En général, nous avons e^{\frac{C_2}{λT}}≫1
Donc, la loi de Planck devient :
\boxed{M_{λT}= C_1*λ^{-5}*e^{-\frac{C_2}{λT}}}
La prise de mesure de la température d’un corps réel
Dans le cadre d’un mesurage effectué avec une caméra IR, nous savons qu’une partie du rayonnement émit par le corps réel traverse l’atmosphère (l’environnement entre le corps étudié et l’objectif), l’objectif de la caméra et vient percuter le détecteur d’une matrice de détection dans notre cas ici avec le module FLIR Lepton 3.5. Ce détecteur absorbe le rayonnement et fournit une tension destinée à être traitée puis traduite en valeur de température.
Plusieurs facteurs influent sur le calcul de la température :
- La distance objet-caméra
- L’humidité relative de l’atmosphère
- La température de l’environnement
- La température ambiante
- La température de l’optique (c’est assez rare que cela soit réellement nécessaire)
- Le facteur de transmission d’une ou plusieurs lentilles additionnelles
- Le facteur de transmission de l’ensemble optique
Il est important que la caméra IR soit caractérisée et étalonnée pour que l’on connaisse son rôle dans la prise de mesure.
Comme évoqué plus tôt, le module FLIR Lepton 3.5 possède une matrice de détection. Cela correspond à un ensemble de détecteurs, placés en ligne et en colonne. Ici, elle est de 160×120.
L’optique d’entrée de la caméra focalise l’image du plan corps sur toute la surface. Chacun des détecteurs de la matrice de détection est relié à un registre mémoire CCD interne. Cela permet de prélever l’information pour lire et traiter.
Conclusion
Nous venons de voir ensemble les principes de fonctionnement d’une caméra IR. Cependant, il est important de faire le lien entre cet aspect théorique et notre module FLIR Lepton 3.5. Nous venons de voir différentes notions qu’il serait judicieux d’exploiter dans le cas de notre projet ou à l’avenir. Tout d’abord, la notion d’espace. En effet, nous savons maintenant que la position de notre module par rapport à l’objet étudié ainsi que la distance qui les sépare influent sur la température perçue. Donc suivant le degré de précision voulu ou les caractéristiques de l’objet étudié, notre module doit pouvoir s’adapter ou/et compenser certaines incertitudes liées à l’espace. De plus, dans l’optique de coupler ce module avec une caméra classique, l’angle d’orientation du module aura un véritable impact sur les données récoltées. Ensuite, la notion de matériaux. Nous venons de voir que suivant le corps étudié, l’émissivité varie. Il serait donc louable de créer dans l’interface, la possibilité de choisir l’émissivité via le matériaux mesuré et donc d’obtenir une température plus proche de la réalité.
Les sources de cette recherche bibliographique sont disponibles à la page « Les sources ».